Having considered localization in practice, we now extend in-plane localization to include a dimension for position determination in space. First, we will specifically highlight the challenges in determining z-coordinates and show ways to overcome them. We will then illustrate the transition of ToF circles into spheres and TDoA hyperbolas into hyperboloids.
General
Usually, our satellites are located at the same and fixed height above objects to be tracked. In three-dimensional reality, our tag is therefore located below a plane spanned by the satellites. This was already true in the previous chapters, where we considered only 2D localization. There, in a simplified form, we made a projection of the satellite plane onto the xy-plane of the tag(s). For most applications, position determination in xy-coordinates is quite sufficient. We achieve accuracies for xy-coordinates of 5-50cm. In reality, however, we are of course in three-dimensional space, in which our RTLS also determines z-coordinates.
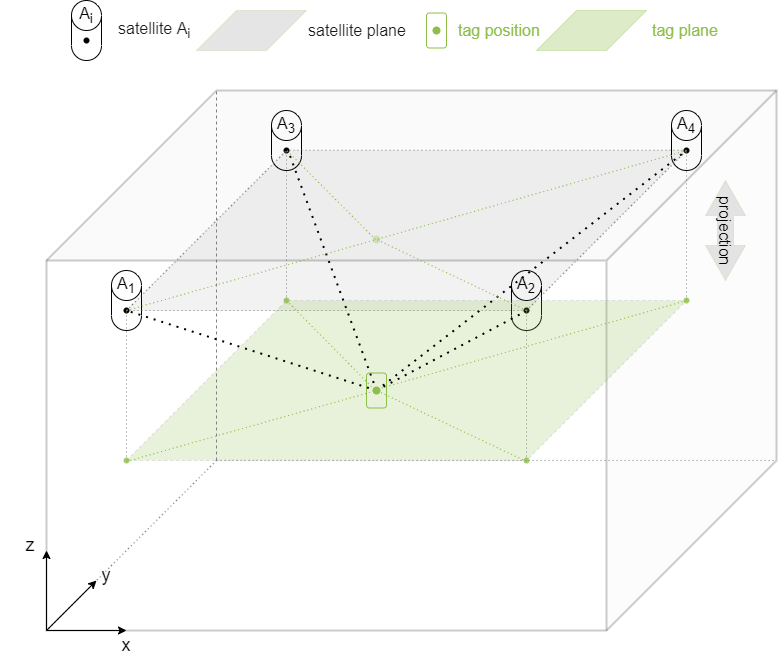
Challenges in z-coordinate determination
The fact that the satellites are located above the tag has the advantage that for ranging in the UWB, ideally there are always Line Of Sight (LOS) connections between the tag and the satellites and thus the signal is not disturbed or attenuated by additional obstacles. However, it makes the determination of the altitude (localization in z-direction) more complex compared to a spatial satellite array.
Satellites on the ground
A spatial satellite array could be implemented with placement of the satellites on the ground. This would offer a possibility to increase the accuracy of the z-coordinate. Practicality of this option is limited, because often obstacles near the ground hinder the “line of sight” (LOS) from tag to satellite. Especially in the UWB this leads to drastic signal strength reduction. However, this must also be taken into account in the 2.4GHz ISM band, since the synchronization of the satellites in such an arrangement would possibly have to be implemented wireless. In an industrial environment, there is also always the risk of physical damage from factory parts. It would be conceivable to include satellites on a lower floor (e.g. office environment) in the ranging, although the signal attenuation due to walls is not negligible.
Satellite spacing
In particular, the distance between the satellites has an influence on the precision of the z-coordinate. The deviations from the real value of z become larger with increasing satellite distance. Of course, this also applies to xy-coordinates, so that a compromise between precision and economy (number of satellites) must always be found.
![]()
Precision increase by fixed z-coordinate?
The decisive factor for all RTL systems is the position accuracy. Assuming that a determination in xy-coordinates is sufficient in the application, there is the option to assign a fixed value to the z-coordinate. This can be done if a tag is attached to mobile workpieces (equipment on wheels, trolleys, etc.), for example. The z-coordinate is then known and constant.
The idea: If the z-value should be subject to strong deviations, we fix the value, in order to be able to determine x- and y-coordinate possibly even more precisely.
In practice, the exact opposite happens, which is illustrated by the following figure
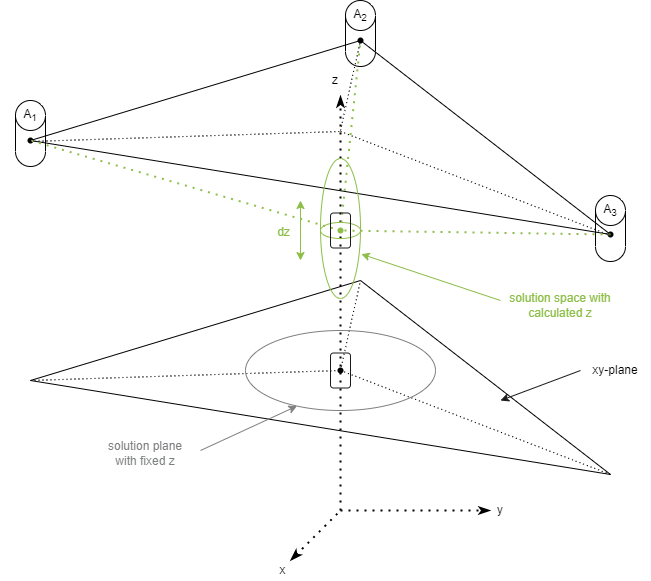
Although the position estimation algorithm is given a constant z-value and “only” needs to calculate x- and y-coordinates, we are thus restricting the possible solution space for position estimation to an xy-plane. This may cause x- and y-values to deviate more from the true value than when including a variable z in the calculation. With variable z-value it is therefore possible to get more precise xy- to the detriment of possible, more inaccurate z-coordinates.
3D localization
With the additional dimension, the geometric entities in both the ToF and TDoA methods also expand by one dimension.
Time of Flight (ToF) in 3D
The circles described in 2D (locations of equal distance between tag and satellite) become spheres in three-dimensional space. We obtain an intersection circle as possible locations for the tag with 2 satellites. The third satellite brings two more intersection circles and they again provide 2 intersection points, thus 2 positions where our object to be tracked could be.
So where is our tag located? The exclusion is done by 2 variants:
- Exclusion by causality: We know that our tag can only be located below the satellite plane. All possible solutions (which are mirrored at the satellite plane) above are ignored.
E.g. GPS: the GPS receiver is logically located near the earth and not outside the stratosphere. - Inclusion of a fourth (or more) satellite, which is the rule in practice, resulting in a unique solution (only one intersection).
The principle can be reproduced by pressing the ▶/ǁ - button. The view can be rotated by mouse.
Time Difference of Arrival (TDoA) in 3D
Similar to the ToF method, the hyperbolas in 2D become three-dimensional objects: Hyperboloids. This is illustrated by the following figure.

source: GPSWorld.com from WONG, S., et al. A Geometric Approach to Passive Target Localization. 2017.
The intersection point is unique, so that 3 hyperboloids and thus 3 satellites are sufficient for the determination of the x-, y- and z-coordinate. As with the ToF method, the localization becomes more precise with each additional satellite.
Conclusion and summary
In the three-part series on localization methods, we gave you a behind-the-scenes look at the ZIGPOS RTLS. We explained the basic principles of the ToF and TDoA methods in the 2D and 3D case and how we realize this with our hardware in practice.
We will continue to be your partner for real-time localization. Innovative, secure, efficient - these are our principles that shape our corporate philosophy and with which we actively work on the development and improvement of the standard as part of the omlox consortium. In this way, we accompany you and your company on the path to Industry 4.0.
