Nachdem wir die Lokalisierung in der Praxis betrachtet haben, erweitern wir nun die Lokalisierung in der Ebene um eine Dimension für die Positionsbestimmung im Raum. Zunächst werden wir konkret die Herausforderungen bei der Bestimmung von z-Koordinaten beleuchten und Möglichkeiten zu deren Bewältigung zeigen. Anschaulich wird danach der Übergang der ToF-Kreise in Kugeln und der TDoA-Hyperbeln in Hyperboloide dargestellt.
Allgemeines
Üblicherweise befinden sich unsere Satelliten in gleicher und fester Höhe oberhalb zu trackender Objekte. Unser Tag befindet sich in der dreidimensionalen Realität also unterhalb einer von den Satelliten gespannten Ebene. Dies galt bereits in den vorangegangen Kapiteln, in denen wir ausschließlich die 2D-Lokalisierung betrachtet haben. Dort haben wir in vereinfachter Form eine Projektion der Satellitenebene auf die xy-Ebene des (der) Tags vorgenommen. Für die meisten Anwendungen ist die Positionsbestimmung in xy-Koordinaten völlig ausreichend. Wir erreichen damit Genauigkeiten für xy-Koordinaten von 5-50cm. In Wahrheit befinden wir uns aber natürlich im dreidimensionalen Raum, in der unser RTLS ebenfalls z-Koordinaten bestimmt.
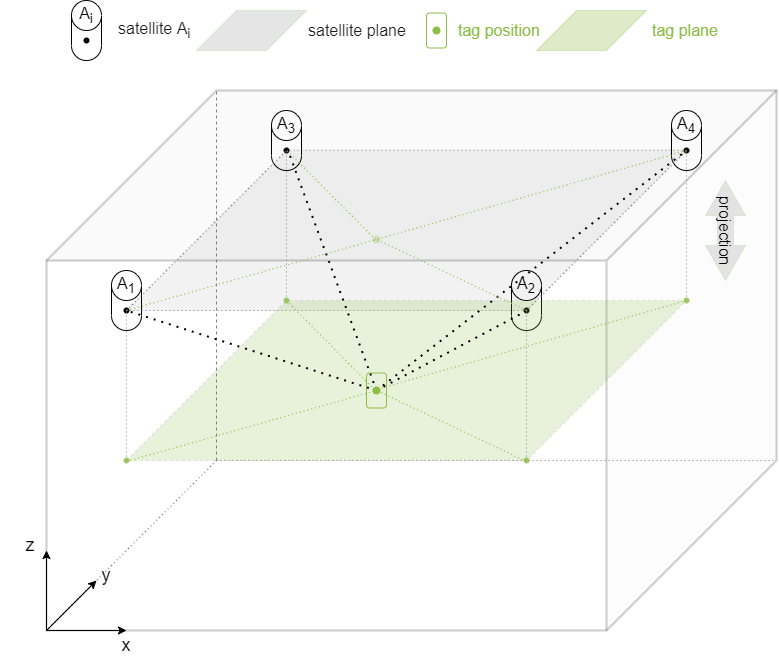
Herausforderungen bei der z-Koordinatenbestimmung
Dass sich die Satelliten über dem Tag befinden, hat zwar den Vorteil, dass für das Ranging im UWB idealerweise stets Line Of Sight (LOS)-Verbindungen zwischen Tag und Satelliten bestehen und so das Signal nicht durch zusätzliche Hindernisse gestört bzw. gedämpft wird. Es macht die Bestimmung der Höhe (Lokalisierung in z-Richtung) jedoch komplexer im Vergleich zu einer räumlichen Satellitenanordnung.
Satelliten am Boden
Eine räumliche Satellitenanordnung könnte mit einer Platzierung der Satelliten am Boden realisiert werden. Dies würde eine Möglichkeit bieten, die Genauigkeit der z-Koordinate zu erhöhen. Praxistauglich ist diese Option nur bedingt, da oft Hindernisse in Bodennähe die „Sicht“ (LOS) von Tag zu Satellit behindern. Gerade im UWB führt dies zu drastischer Signalstärkereduktion. Zu berücksichtigen ist dies jedoch auch im 2.4GHz ISM-Band, da die Synchronisation der Satelliten in einer derartigen Anordnung womöglich wireless realisiert werden müsste. In industrieller Umgebung ist zudem stets die Gefahr einer physischen Beschädigung durch Werkteile gegeben. Denkbar wäre die Möglichkeit, Satelliten einer unteren Etage (z.B. Büroumgebung) in das Ranging einzubeziehen, wobei die Signaldämpfung durch Wände nicht vernachlässigbar ist.
Satellitenabstand
Einfluss auf die Präzision der z-Koordinate hat insbesondere auch der Abstand der Satelliten zueinander. Die Abweichungen vom Realwert von z werden mit zunehmendem Satellitenabstand größer. Das gilt selbstverständlich auch für xy-Koordinaten, sodass immer ein Kompromiss zwischen Genauigkeit und Wirtschaftlichkeit (Satellitenanzahl) gefunden werden muss.
![]()
Präzisionserhöhung durch fixierte z-Koordinate?
Entscheidend bei allen RTL-Systemen ist die Positionsgenauigkeit. Unter der Annahme, dass eine Bestimmung in xy-Koordinaten im Anwendungsfall ausreichend ist, gibt es die Option, der z-Koordinate einen festen Wert zuzuweisen. Dies kann getan werden, wenn ein Tag z.B. an mobilen Werkteilen (Geräte auf Rädern, Rollwagen etc.) angebracht ist. Die z-Koordinate ist dann bekannt und konstant.
Der Gedanke: Sollte der z-Wert starken Abweichungen unterliegen, fixieren wir den Wert, um x- und y- Koordinate eventuell sogar präziser bestimmen zu können.
In der Praxis erfolgt das genaue Gegenteil, was folgende Abbildung illustriert
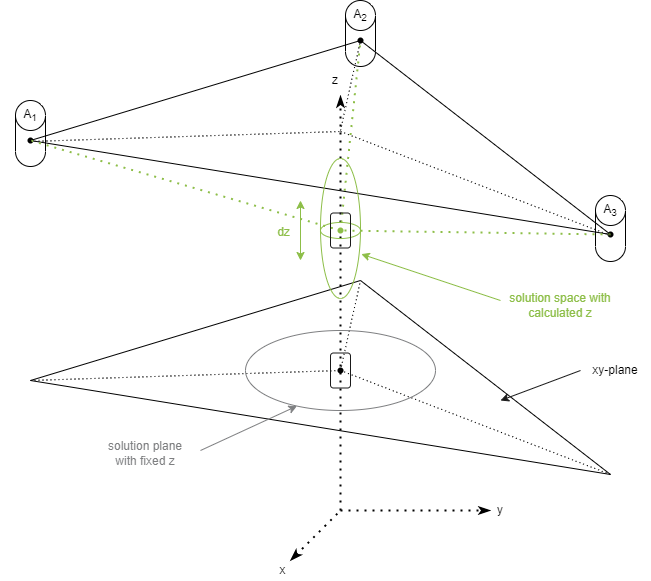
Zwar erhält der Algorithmus zur Positionsabschätzung einen konstanten z-Wert und muss „nur noch“ x- und y-Koordinaten berechnen, jedoch schränken wir damit den möglichen Lösungsraum für die Positionsabschätzung auf eine xy-Ebene ein. Dies kann dazu führen, dass x- und y-Werte stärker vom wahren Wert abweichen als unter Einbezug eines variablen z in den Berechnung. Mit variablem z-Wert ist es also möglich, präzisere xy- zum Nachteil möglicher, ungenauerer z-Koordinaten zu erhalten.
Lokalisierung in 3D
Mit der zusätzlichen Dimension erweitern sich auch die geometrischen Gebilde beim ToF- als auch beim TDoA-Verfahren um eine Dimension.
Time of Flight (ToF) in 3D
Aus den in 2D beschriebenen Kreisen (Orte gleicher Entfernung zwischen Tag und Satellit) werden Kugeln im dreidimensionalen Raum. Wir erhalten als mögliche Orte für das Tag mit 2 Satelliten einen Schnittkreis. Der dritte Satellit bringt zwei weitere Schnittkreise und die liefern wiederum 2 Schnittpunkte, also 2 Positionen, an denen sich unser zu trackendes Objekt befinden könnte.
Wo befindet sich also unser Tag? Der Ausschluss erfolgt durch 2 Varianten:
- Ausschluss durch Kausalität: Wir wissen, dass sich unser Tag nur unterhalb der Satellitenebene befinden kann. Alle möglichen Lösungen (die an der Satellitenebene gespiegelt sind) oberhalb werden ignoriert.
Bsp. GPS: der GPS-Empfänger befindet sich logischerweise in Erdnähe und nicht außerhalb der Stratosphäre - Einbeziehung eines vierten (oder mehr) Satelliten, was in der Praxis die Regel ist, sodass eine eindeutige Lösung (nur ein Schnittpunkt) entsteht.
Das Prinzip kann durch Drücken des ▶/ǁ - Buttons nachvollzogen werden. Die Ansicht ist per Maus drehbar.
Time Difference of Arrival (TDoA) in 3D
Ähnlich dem ToF-Verfahren werden aus den Hyperbeln in 2D drei-dimensionale Objekte: Hyperboloide. Anschaulich macht dies folgende Abbildung.

Quelle: https://www.gpsworld.com/wp-content/uploads/2018/02/Jones-Feb-3.jpg aus WONG, S., et al. A Geometric Approach to Passive Target Localization. 2017.
Der Schnittpunkt ist eindeutig, sodass 3 Hyperboloide und damit 3 Satelliten für die Bestimmung der x-,y- und z-Koordinate ausreichend sind. Präziser wird die Lokalisierung natürlich wie beim ToF-Verfahren mit jedem weiteren Satelliten.
Fazit und Zusammenfassung
In der dreiteiligen Serie zu Lokalisierungsmethoden haben wir Ihnen einen Einblick hinter die Kulissen des ZIGPOS RTLS gegeben. Wir haben Ihnen die Grundprinzipien der ToF- und TDoA-Verfahren im 2D- und 3D-Fall erläutert und wie wir dies mit unserer Hardware in der Praxis realisieren.
Wir sind auch in Zukunft Ihr Partner für Echtzeit-Lokalisierung. Innovativ, sicher, effizient - Dies sind unsere Prinzipien, die unsere Unternehmensphilosophie prägen und mit denen wir als Teil des omlox Konsortiums aktiv an der Entwicklung und Verbesserung des Standards arbeiten. Damit begleiten wir Sie und Ihr Unternehmen auf dem Weg zur Industrie 4.0.
