Im folgenden Beitrag werden Grundlagen und Prinzipien von Ranging-Verfahren erläutert und ein Überblick zu den Lokalisierungmethoden im Ultra-Breitband (Ultra-wideband - UWB) gegeben. Wir beschreiben zudem deren Integration im ZIGPOS RTLS. Der Beitrag erstreckt sich auf 3 Teile:
- Dieser erste Teil beschränkt sich auf die Lokalisierung in der Ebene (2D) und dessen Grundprinzipien.
- In einer Fortsetzung wird dann die Realisierung im ZIGPOS RTLS beschrieben.
- Der letzte Teil betrachtet die Lokalisierung im Raum (3D) und geht auf deren Herausforderungen sowie Lösungsmöglichkeiten ein.
Zielstellung
Das Ziel aller Lokalisierungsmethoden ist die Ortsbestimmung eines ruhenden oder sich bewegenden Objekts. Das Ergebnis des Ortungsprozesses ist eine üblicherweise dreidimensionale Positionsangabe in einem relativen, räumlichen Bezugssystem oder erdfesten Referenzsystem (Geo-Koordinaten).
In diesem ersten Teil beschränken wir uns jedoch auf die Positionsbestimmung in der Ebene, da sich die Prinzipien der Methoden verständlicher erläutern und abbilden lassen. Im Allgemeinen kann Lokalisierung als zwei- bzw. mehrstufiges Verfahren betrachtet werden, bei dem im ersten Schritt eine relative Positionsangabe aus Ranging-Werten, die auf Zeitstempeln oder Zeitdifferenzen beruhen, ermittelt wird. Diese relative Positionsangabe besitzt einen Raumbezug zu einem hierarchisch übergeordneten Bezugssystem bzw. zu absoluten Referenzpositionen, sodass im zweiten bzw. weiteren Schritten eine Transformation in das übergeordnete Bezugssystem bis hin zu absoluten Geo-Koordinaten erfolgen kann und wir eine absolute Position auf der Erdoberfläche erhalten.
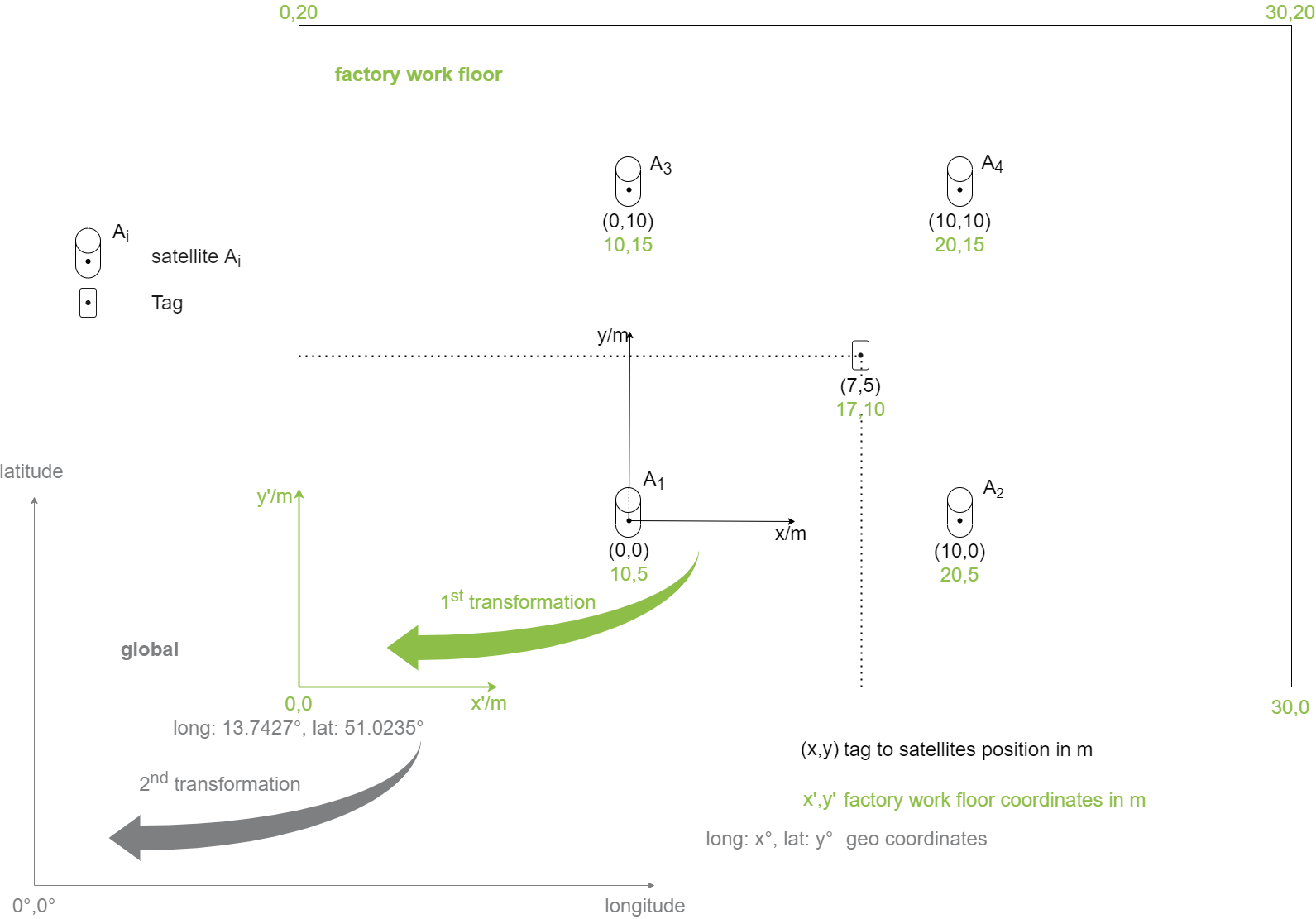
Beispiel Werkshalle: Zunächst wird über ein gewähltes Ranging-Verfahren die Position eines Werkzeuges innerhalb der Werkshalle ermittelt. Dies kann z.B. über mehrere Distanzmessungen des Werkzeugs zu festen Referenzpositionen, Satelliten Ai, erfolgen. Die ermittelten Koordinaten, z.B. x=17m, y=10m des Werkzeugs geben die relative Position des Werkzeugs innerhalb der Werkhalle mit Koordinatenursprung in einer der Ecken an. Der Koordinatenursprung der Halle selbst besitzt wiederum absolute Geo-Koordinaten, sodass über Transformation dem Werkteil eine absolute Position auf der Erdoberfläche zugeordnet werden kann.
Im engeren Sinn ist bereits die Position des mobilen Objekts, Tag, zu den Satelliten als relative Position zu betrachten. Die erste Transformation findet demnach bereits vom Tag-zu-Satelliten-Koordinatensystem in die Hallenkoordinaten statt. Dieser Schritt ist für die industrielle Ortung in der Regel genügend.
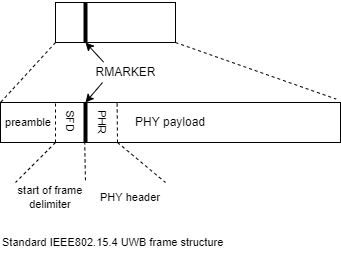
Aufbau einer UWB-Nachricht
Zur Lokalisierung von Objekten im UWB werden mehrere Nachrichten zwischen für die Ortung notwendigen Geräten ausgetauscht. Diese beinhalten für Lokalisierung entscheidenden Informationen. Für das Senden und Empfangen einer Nachricht im UWB werden zwei Geräte benötigt, wobei eines die Funktion des Senders (Transmitter), das andere die des Empfängers (Receiver) übernimmt. In der Regel sind beide Gerät in der Lage, Nachrichten zu senden und empfangen. Man bezeichnet sie daher als Transceiver. Die Grundstruktur der UWB-Nachrichten regelt IEEE802.15.4 und sieht wie folgt aus.
Time of Arrival (ToA)
Der RMARKER in der Sender- und Empfängernachricht markiert zeitlich das Ende der Preamble und den Beginn des Datenpakets (Payload). Er wird als Zeitstempel (timestamp) gespeichert und kann im Payload übertragen werden. Der Zeitpunkt, an dem der RMARKER an der Empfangsantenne detektiert wird, wird als Time of Arrival (ToA) bezeichnet
Signallaufzeit - Time of Flight (ToF)
Um Distanzen zwischen Sendern und Empfängern zu ermitteln, bildet in UWB-basierten RTL-Systemen die Messung der Signallaufzeit die Grundlage. Die Laufzeit, die ein Signal von Sender- zu Empfängerantenne benötigt, wird als Time of Flight (ToF) bezeichnet und über die Differenz der Zeitstempel an Sende- und Empfangsantenne bestimmt. Die Signale selbst bewegen sich als elektromagnetische Wellen annähernd mit Lichtgeschwindigkeit c durch den Raum.
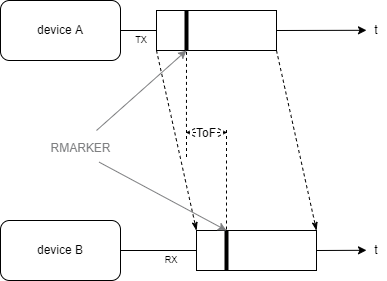
Sind Sende- und Empfangszeitpunkt bekannt, kann über die Signallaufzeit (ToF) die Distanz zwischen Sender und Empfänger ermittelt werden:
$$ D = c \cdot \text{ToF} $$
Wird wie im obigen Bild nur eine Nachricht von Gerät A zu Gerät B übertragen spricht man vom One-Way-Ranging, das äußerst präzise Zeitsynchronisation zwischen Sender und Empfänger erfordert. Erweiterungen dieser einfachen Variante werden folgend erläutert.
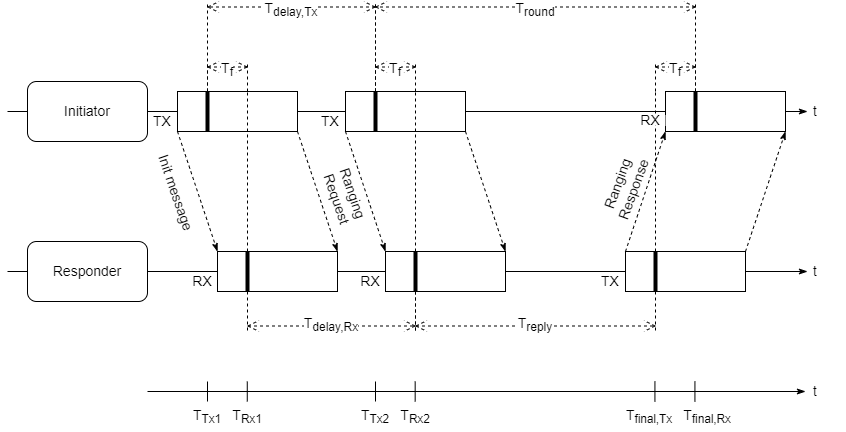
Single-Sided Two-Way-Ranging (SS-TWR)
Bei diesem Verfahren initiiert der Sender die Distanzbestimmung mit einem Ranging-Request an den Empfänger, den dieser nach der ToF (TF) empfängt und mit der Antwortverzögerung Treply dem Initiator antwortet. Dieser sogenannte Round-Trip ist nach der Zeit Tround abgeschlossen und die Distanz kann ermittelt werden:
$$ D = \frac{c}{2} \cdot (T_\text{round}-T_\text{reply}) $$
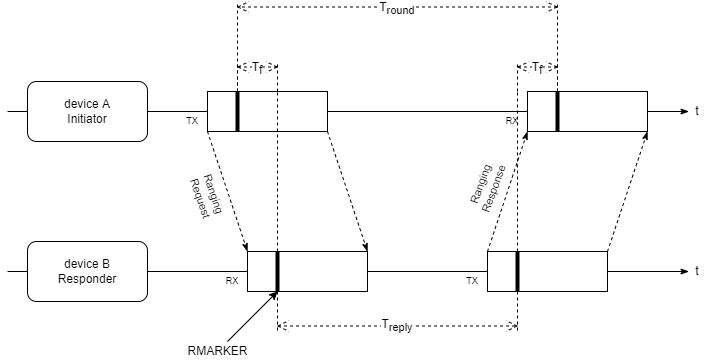
Da es sich um ein asynchrones, asymmetrisches Verfahren handelt und die Takte auf Sender- und Empfängerseite bis zu 20ppm (worst case nach IEEE802.15.4a) vom Nominaltakt abweichen, führt das Verfahren zu einem Taktversatz (Clock Offset) zwischen Sender und Empfänger. Es kann daher zu enormen Abweichungen der ermittelten Entfernung zum wahren Wert führen.
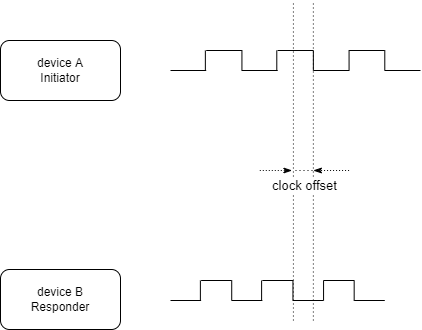
Ein Beispiel: Bei einer Antwortverzögerung von Treply=0,5ms und Taktfrequenz der UWB-ICs von 125MHz erhalten wir für die Abweichung1 der ToF vom wahren Wert: $$\hat T_\text{f} - T_\text{f} = \frac{T_\text{reply}}{2} (e_\text{A}-e_\text{B}) = \frac{0.5 \text{ ms}}{2} \cdot 40 \cdot 10^{-6} = 10 \text{ ns} $$ Dies entspricht einer Distanzabweichung von 3 Metern!
Dieses Problem kann jedoch schrittweise durch bestimmte Verfahren beschränkt werden.
- Detektion:
- Hardware integrierte Clock Offset Ratio (COR) - Detektion des Empfangssignals
- über zusätzliche Zeitmessung kann der Zeitversatz von Sender zu Empfänger bestimmt werden
- Korrektur:
- kann softwareseitig unter Einbezug des ermittelten COR in die Berechnung der Distanz erfolgen
- kann auf Hardwareebene über die Integration eines Voltage Controlled Oscillators (VCO) erfolgen
Beispiele:
- Wird die Hardware integrierte COR-Detektion genutzt, kann dieser Wert über ein Register des UWB-Moduls gelesen werden. Die Berechnung der Distanz erfolgt mit Korrektur des Clock Offsets und ist $$ D = \frac{c}{2} \cdot (T_\text{round}-(1-\text{COR}) \cdot T_\text{reply}) $$
- Senden wir vor dem Round-Trip eine zusätzliche Nachricht an den Responder, können Zeitdifferenzen auf Sender- und Empfängerseite zwischen erster und zweiter Nachricht bestimmt werden. Im zweiten Schritt kann damit ebenfalls das COR bestimmt und die Distanzberechnung korrigiert werden. Folgender Zeitverlauf soll dies veranschaulichen:
Über die Korrektur des COR-Fehlers werden die Zeitbasen des Senders und Empfängers einander angeglichen. Die Distanz lässt sich wie folgt berechnen: $$ D = \frac{c}{2} \cdot (T_\text{round}-(1-\text{COR}) \cdot T_\text{reply})$$ $$= \frac{c}{2} \cdot \left(T_\text{final,Rx}-T_\text{Tx2} - \frac{T_\text{Tx2}-T_\text{Tx1}}{T_\text{Rx2}-T_\text{Rx1}} \cdot (T_\text{final,TX}-T_\text{Rx2})\right)$$
Double-Sided Two-Way-Ranging (DS-TWR)
Das DS-TWR ist eine Erweiterung des SS-TWR um einen zusätzlichen Round-Trip, wobei zunächst Gerät A und im zweiten Round-Trip Gerät B die Rolle des Initiators einnimmt.
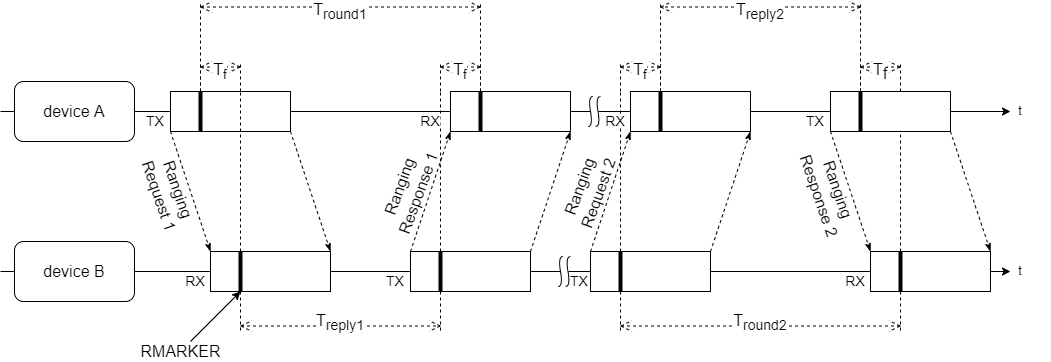
Dabei werden vier Nachrichten zwischen Gerät A und B übertragen, die auf drei reduziert werden können, sodass ein Ranging deutlich schneller und so mehrere Messungen pro Zeiteinheit möglich sind. So kann Ranging Response 1, das Ende des ersten Round-Trips, gleichzeitig den Ranging Request 2 stellen und damit den zweiten Round-Trip einleiten. Im DS-TWR mit drei Nachrichten wird diese Nachricht als Ranging Response bezeichnet. Das Ranging wird mit der finalen Nachricht, die alle gespeicherten Zeitstempel von Gerät A in ihrem Nachrichtenpaket enthält, an Gerät B beendet.
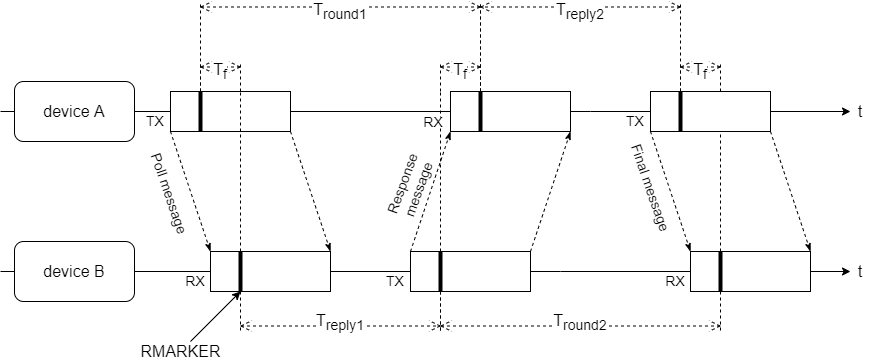
Die Distanz kann für beide Varianten mit
$$ D=\frac{c}{4} \cdot (T_\text{round1}-T_\text{reply1}+T_\text{round2}-T_\text{reply2})$$
bestimmt werden, wobei die Abweichung vom wahren Wert von D proportional zum Taktversatz (eA-eB) zwischen Sender und Empfänger und der Differenz der Antwortverzögerungen (Treply2-Treply1) ist. Das bedeutet, je stärker die Antwortverzögerungen von Sender und Empfänger voneinander abweichen, desto größer ist der Fehler in unserer Distanzberechnung. Die Antwortverzögerungen müssen daher zwingend gleich sein.
Ist dies der Fall, spricht man vom symmetrischen DS-TWR.
Diese Forderung nach Symmetrie ist oft schwer realisierbar. Durch einen rein „mathematischen Trick“ kann die Entfernung zwischen Sender und Empfänger jedoch auch durch
$$ D=c \cdot \left(\frac{T_\text{round1}T_\text{round2}-T_\text{reply1}T_\text{reply2}}{T_\text{round1}+T_\text{reply1}+T_\text{round2}+T_\text{reply2}}\right)$$
bestimmt werden, wobei die strikte Forderung nach Symmetrie entfällt. Die Antwortverzögerungen beider Geräte müssen in dem Fall nicht mehr gleich sein. Man spricht hier vom asymmetrischen DS-TWR Der Distanzfehler ist hier nur noch proportional zum Taktversatz e und beträgt daher maximal 20ppm.
Für weiter Informationen insbesondere zu Formeln und deren Herleitung sei auf folgende Quellen verwiesen:
- D. Neirynck, E. Luk and M. McLaughlin, “An alternative double-sided two-way ranging method,” 2016 13th Workshop on Positioning, Navigation and Communications (WPNC), 2016, pp. 1-4, doi: 10.1109/WPNC.2016.7822844.
- “IEEE Standard for Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications for Peer Aware Communications (PAC), Annex D” in IEEE Std 802.15.8-2017 , vol., no., pp.307-311, 7 Feb. 2018, doi: 10.1109/IEEESTD.2018.8287784.
Zusammenfassung der ToF-Methoden
Folgende Tabelle gibt einen Überblick zu Berechnungen mit Beispielen zu den verschiedenen TWR-Methoden, ihren Eigenschaften mit Vor- und Nachteilen:
| SS-TWR | |||||
|---|---|---|---|---|---|
| symmetrisches | asymmetrisches | ||||
| berechnete ToF: $$ \hat T_\text{f} $$ | $$\frac{1}{2}(T_\text{round}-T_\text{reply})$$ | $$ \frac{1}{4} (T_\text{round1}-T_\text{reply1}+T_\text{round2}-T_\text{reply2})$$ | $$ \hspace{0.2cm} \frac{T_\text{round1}T_\text{round2}-T_\text{reply1}T_\text{reply2}}{T_\text{round1}+T_\text{reply1}+T_\text{round2}+T_\text{reply2}} $$ | ||
| mit COR-Kompensation: $$ \frac{1}{2}(T_\text{round}-(1-\text{COR})\cdot T_\text{reply}) $$ | |||||
| Abweichung1: $$\hat T_\text{f}-T_\text{f}$$ | $$\approx \frac{1}{2}(e_\text{A}-e_\text{B})T_\text{reply}$$ | $$\approx \frac{1}{4}(e_\text{A}-e_\text{B})(T_\text{reply2}-T_\text{reply1})$$ | $$e_\text{A}T_\text{f}=e_\text{B}T_\text{f}$$ | ||
| Abweichung: Beispiel | $$T_\text{reply}=0.5\text{ms}$$ Abweichung: 10ns \( \hat = \) 3m! | $$T_\text{reply2}-T_\text{reply1}=0.1\text{ms}$$ Abweichung: 1ns \( \hat =\) 30cm | $$ \hat T_\text{f}=300\text{ns} \; \hat = \; D=90\text{m}$$ Abweichung: 6ps \( \hat =\) 1.8mm | ||
| Anzahl Nachrichten | 2 o. 3 mit COR-Kompensation | 3 o. 4 | 3 o. 4 | ||
| Präzision | – / + mit COR-Kompensation | + / ++ je nach Symmetrie | ++ | ||
| Vorteile | einfach zu implementieren | höhere Präzision als SS-TWR | hohe Präzision, geringe Anforderung an Synchronität | ||
| Nachteile | große Abweichung ohne COR-Kompensation, strikte Anforderungen an Synchronität | Forderung nach gleichen Antwortverzögerungen erschwert Implementierung | Komplexität im Zeit- und Rechenbedarf | ||
Positionsbestimmung mit ToF
Die Positionsbestimmung eines Tags beruht im 2D-Fall auf einer Kombination von mindestens je einer ToF-Messung zwischen dem Tag und mindestens 3 Satelliten mit ihren jeweiligen Referenzpositionen Ai. Die ermittelten Entfernungen Di zwischen Satellit und Tag ergeben Kreise und bilden Orte gleicher Signallaufzeiten (ToF) ab. Der Schnittpunkt der Kreise bestimmt die Position P des Tags.
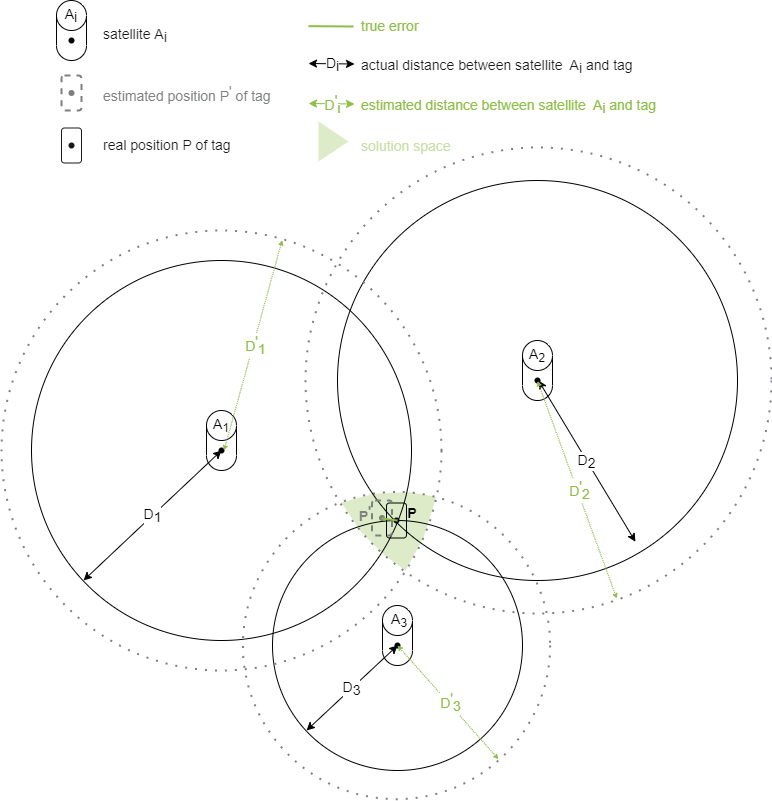
Aufgrund von Messfehlern der Signallaufzeiten z.B. durch den beschriebenen Clock Offset, erhalten wir statt eines Schnittpunktes eine Schnittfläche, die eine Positionsschätzung erlaubt. Die Positionsbestimmung in diesem Lösungsraum erfolgt durch mathematischen Verfahren, bei ZIGPOS z.B. Multi-Dimensionale Skalierung oder probalistisch mittels Monte-Carlo Lokalisierung.
Time Difference of Arrival (TDoA)
Dieses Verfahren beruht im engeren Sinne auf ToA. Der Unterschied zum ToF-Verfahren besteht darin, dass mit den Empfangszeitpunkten an den Satelliten nicht Signallaufzeiten (ToF) zwischen Sender und Empfänger ermittelt werden, sondern Zeitdifferenzen zwischen den jeweiligen Empfangszeitpunkten an den Empfängern. Ein Vorteil dabei ist, dass der (die) Sendezeitpunkt(e) nicht bekannt sein und damit Tags und Satelliten nicht zwangsläufig taktsynchron arbeiten müssen. Satelliten untereinander müssen jedoch äußerst präzise (in UWB-Zeitperioden von 15.65ps) miteinander synchronisiert werden.
Da es sich um Zeitdifferenzen handelt, benötigt man für eine „Entfernungsbestimmung“, anders als beim TWR, mindestens 3 Transceiver, ein Tag und mindestens 2 Satelliten. Wobei der Begriff „Entfernung“ hier nicht korrekt ist. Denn eine konstante Distanz wie beim ToF-Verfahren zu einem bestimmten Satelliten lässt sich mit dem Verfahren nicht ermitteln. Es handelt sich viel mehr um Orte gleicher Signallaufzeitdifferenzen und damit gleichen Entfernungsunterschieden zu zwei Satelliten. Diese Orte lassen sich wie folgt bestimmen:
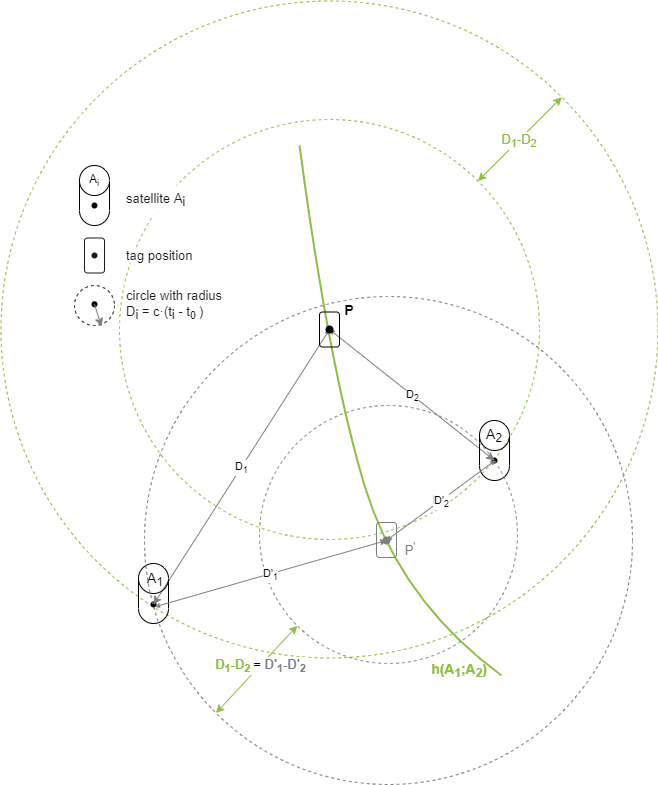
Das Tag sendet ein Signal zum unbekannten Zeitpunkt t0, welches an Satellit Ai zum Zeitpunkt ti und an Satellit Aj zum Zeitpunkt tj detektiert wird. Es ergeben sich jeweils Kreise mit den Radien Di und Dj; im folgenden Bild dargestellt. Zwar ändern sich die einzelnen Radien auf der Hyperbel, die Differenz der Radien ist jedoch konstant.
Noch einmal: Die eingezeichneten Radien (Distanzen von Tag zu Satellit) sind einzeln aufgrund der unbekannten Sendezeit nicht bestimmbar!
$$ h(A_\text{i};A_\text{j}): D_\text{i}-D_\text{j}=c \cdot (t_\text{i}-t_\text{0}) - c \cdot (t_\text{j}-t_\text{0}) = c \cdot (t_\text{i}-t_\text{j}) = \text{const.}$$
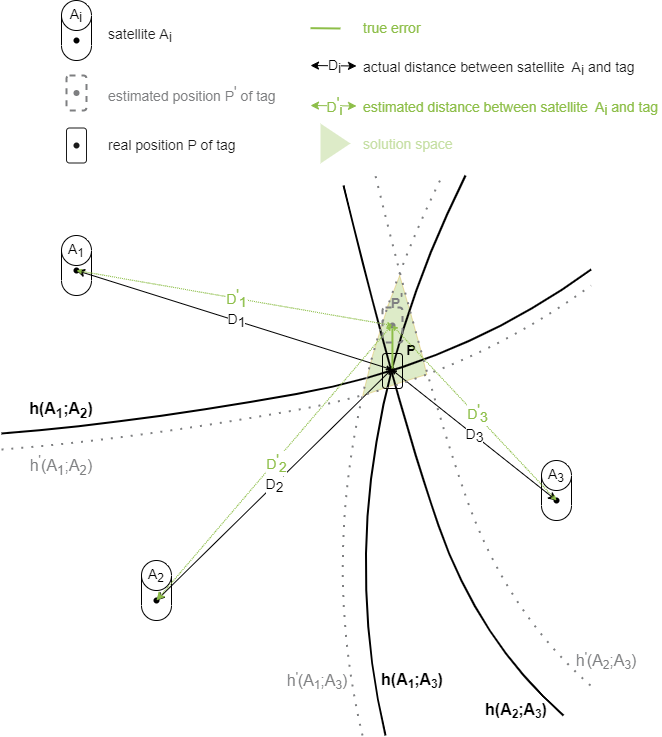
Positionsbestimmung mit TDoA
Wie beim ToF-Verfahren sind für die Lokalisierung eines Tags mindestens 3 Satelliten mit ihren Referenzpositionen Ai im 2D-Fall nötig. Die Hyperbeln h(Ai;Aj) kennzeichnen wie zuvor beschrieben die Orte gleicher Zeitdifferenzen zwischen Satellit Ai und Aj. Zur Lokalisierung des Tags sind 2 Hyperbeln hinreichend, da sie einen eindeutigen Schnittpunkt ergeben. Zwangsläufig resultieren aus einer Messung mit 3 Satelliten jedoch 3 Hyperbeln, sodass alle drei in die Positionsberechnung einfließen. Wie beim ToA-Verfahren beeinflussen Messfehler h’(Ai;Aj) die Abschätzung der Tag-Position.
Zum Verständnis, wie sich die Hyperbeln abhängig von der Tag- und Satellitenposition entwickeln, dient folgendes interaktive GeoGebra Applet:
Die verwendeten Applets basieren auf dem Anritsu TDOA simulation tool (Vers. 0.9) by Ferdinand Gerhardes.
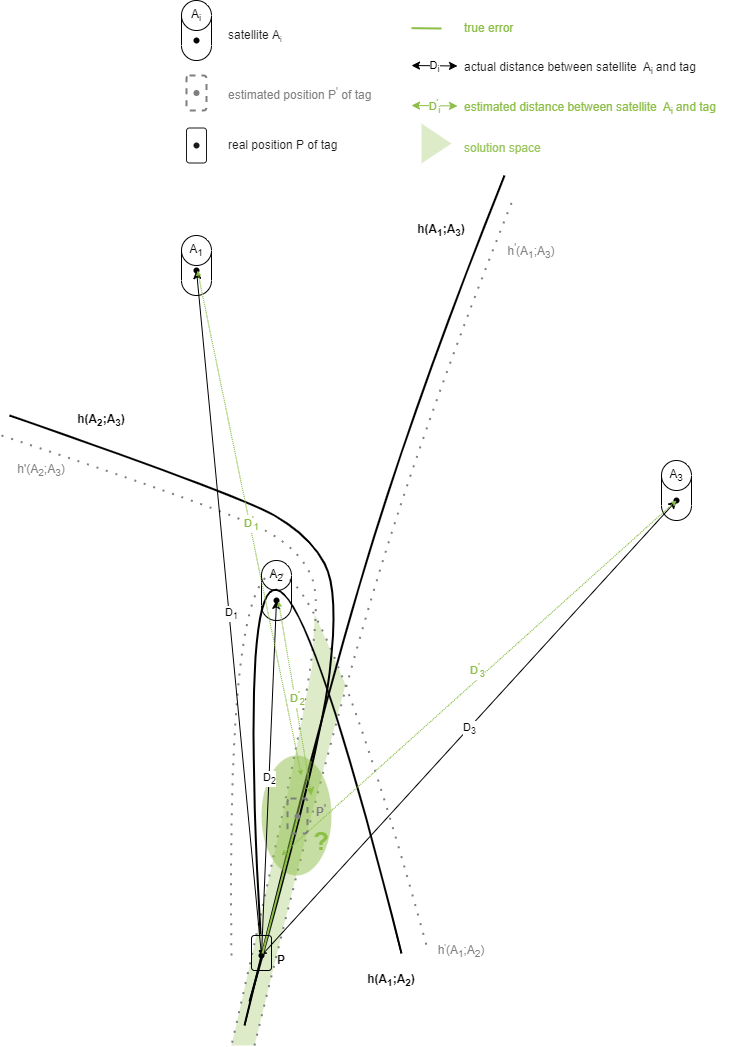
Robustheit
Im Vergleich zum ToF- ist das TDoA-Verfahren für Fehler im Randbereich der Satelliten äußerst anfällig. Der Fehlerbereich bzw. Lösungsraum zur Positionsschätzung wird außerhalb der Satellitenradien immer größer. Grund ist die Herausforderung bei der Bestimmung der Hyperbelschnittpunkte. Da der Lösungsraum beim ToF mithilfe von Kreisen bestimmt wird, ist die Positionsschätzung im Randbereich wesentlich genauer als beim TDoA. Die nachfolgende Abbildung verdeutlicht dies.
Fazit und Zusammenfassung
In diesem Teil wurden grundlegende Verfahren zur Distanzbestimmung zwischen Sendern und Empfängern beschrieben. Diese beruhen auf Signallaufzeiten bzw. deren Differenzen. Die Lokalisierung erfolgt beim ToF über Orte gleicher Signallaufzeiten zum Satelliten (Kreisen) und beim TDoA auf Orten gleicher Signallaufzeitdifferenzen zwischen Satellitenpaaren (Hyperbeln). Die Verfahren zur Ermittlung der Signallaufzeiten sind unterschiedlich komplex und unterscheiden sich in ihren Genauigkeiten auch in Abhängigkeit der Topologie.
Wir von ZIGPOS entwickeln unser RTLS stets im Interesse unserer Kunden weiter. Dabei stehen neben Präzision, die Zuverlässigkeit und Schnelligkeit unseres RTLS für Ihre Zufriedenheit stets im Vordergrund!
Lesen Sie im folgenden Part, wie wir Lokalisierung mit dem ZIGPOS RTLS umsetzen.